算法之路

算法学习笔记

本笔记主要记录一些算法学习过程中的记录和学习疑难点，并非学习资源

学习资源推荐：

https://www.hello-algo.com/chapter_preface/about_the_book/#012

1hello 算法

关于书籍内容和大纲

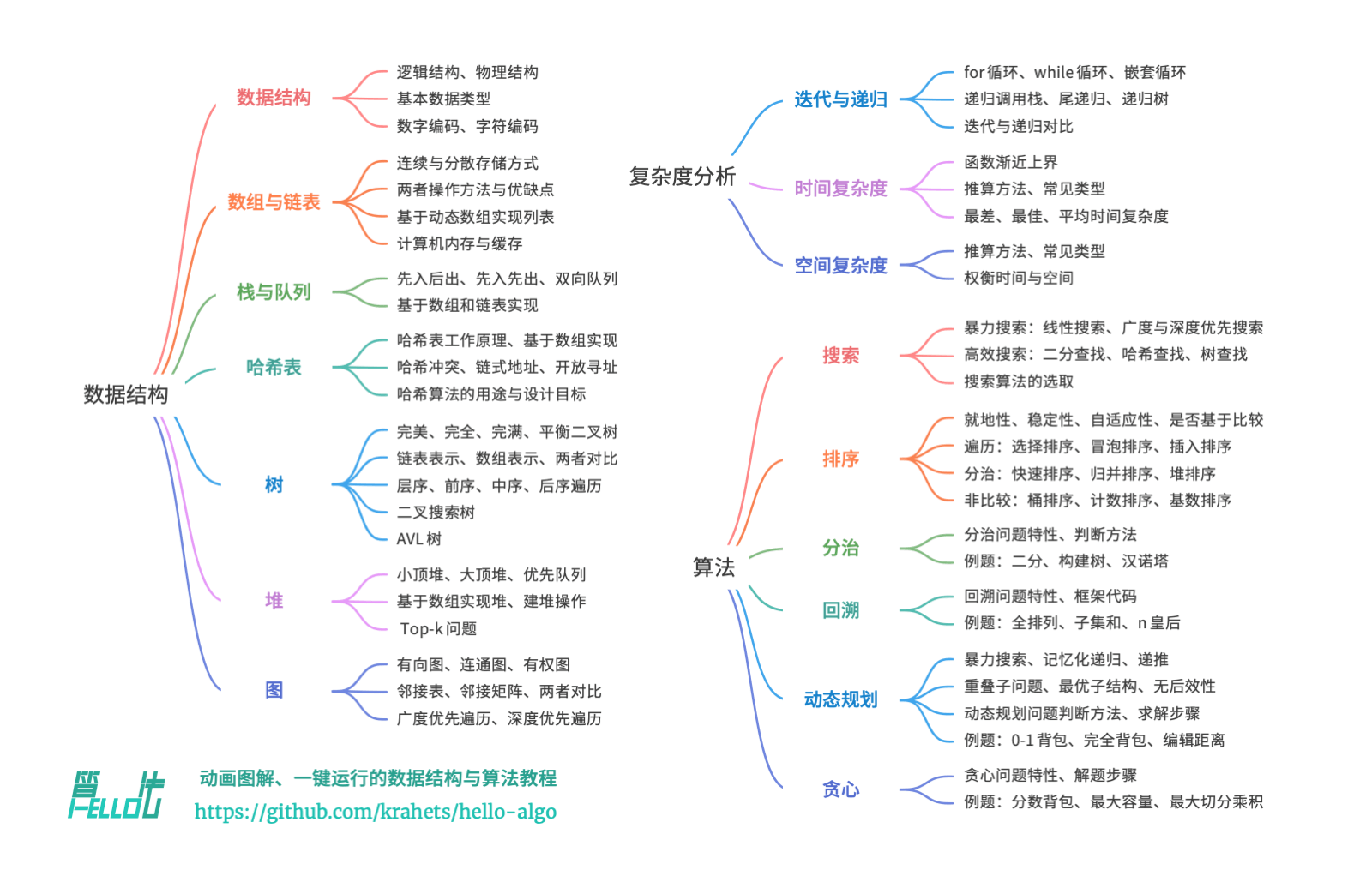
算法的实际例子：

1. 查字典 二分
2. 打扑克 插入排序
3. 货币找零 贪心

算法的定义：==有限== 时间内解决问题的一组指令

有以下特性：

• 时间/ 输入/输出明确
• 可行性
• 有确定含义

数据结构定义：组织和存储数据的方式， 涵盖数据内容/ 数据之间关系和数据操作

设计目标：

• 空间少
• 操作简单快速
• 简洁逻辑

一方面提升另一方面妥协：

• 链表 – 访问慢 新增和删除快
• 数组 相反

Todo: 这里删除节点快是指中间的也快吗？

删除已知节点，通常需要先进行查找，对于数组和链表来说

数据结构与算法的关系

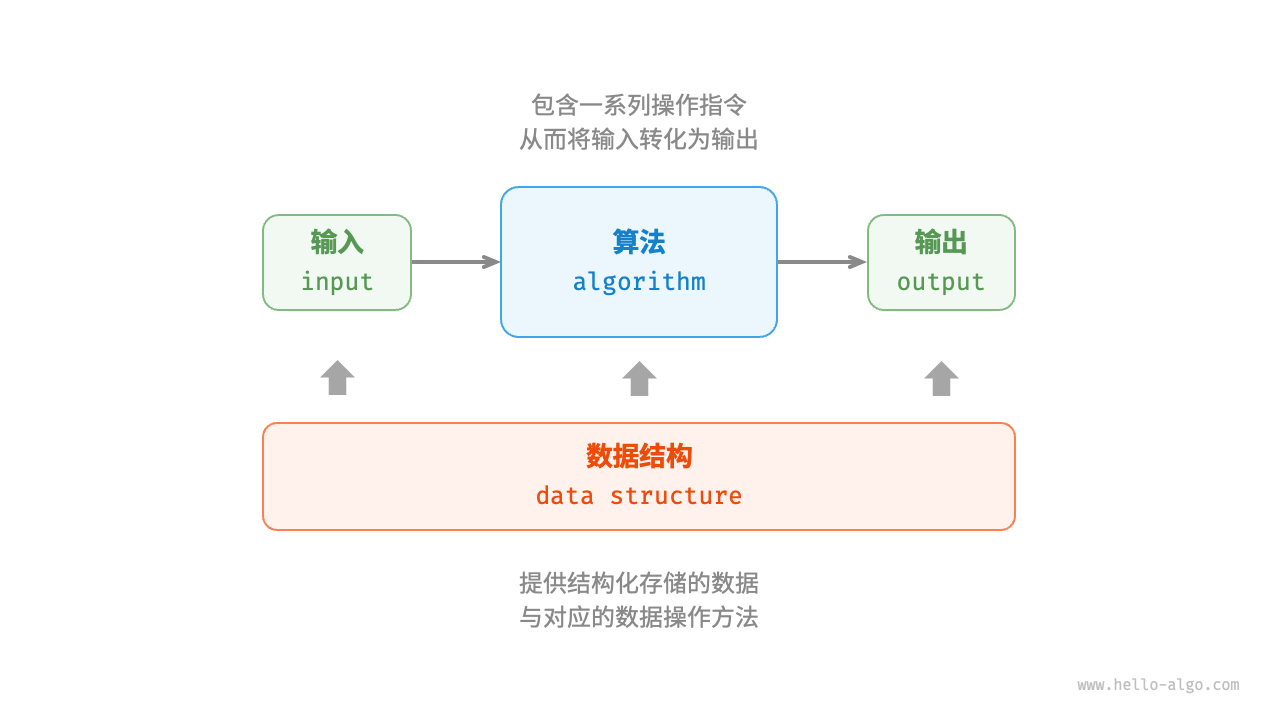
• 数据结构是算法的基石
• 算法是数据结构发挥作用的舞台
• 算法基于不同的数据结构实现 ==> 选择合适的 数据结构是关键

学习算法的意义 ：

Q：作为一名程序员，我在日常工作中从未用算法解决过问题，常用算法都被编程语言封装好了，直接用就可以了；这是否意味着我们工作中的问题还没有到达需要算法的程度？

如果把具体的工作技能比作是武功的“招式”的话，那么基础科目应该更像是“内功”。

我认为学算法（以及其他基础科目）的意义不是在于在工作中从零实现它，而是基于学到的知识，在解决问题时能够作出专业的反应和判断，从而提升工作的整体质量。举一个简单例子，每种编程语言都内置了排序函数：

• 如果我们没有学过数据结构与算法，那么给定任何数据，我们可能都塞给这个排序函数去做了。运行顺畅、性能不错，看上去并没有什么问题。
• 但如果学过算法，我们就会知道内置排序函数的时间复杂度是 𝑂(𝑛log⁡𝑛) ；==而如果给定的数据是固定位数的整数（例如学号），那么我们就可以用效率更高的“基数排序”来做，将时间复杂度降为 𝑂(𝑛𝑘)==，其中 𝑘 为位数。当数据体量很大时，节省出来的运行时间就能创造较大价值（成本降低、体验变好等）。

2算法复杂度

• 算法效率评估
• 迭代与递归
• 时间复杂度
• 空间复杂度
• 小结

1. 什么是实际测量，什么是理论测量？
2. 如何计算常见的时间复杂度？

递归和迭代 2.2

1. for 循环 while 循环的使用场景的区别？
2. 循环和递归方法更节省内存？
3. 递归最常见的是什么错误？如何改进递归？
4. 简单写一个递归函数，并进行改进
5. 递归树是什么？ 如何写一个递归树？
6. 递归和迭代分别适用于什么问题？其区分主要考虑哪几个要素？
7. 迭代和递归有什么内在联系？如何将递归操作转换为迭代的操作？具体写代码如何表示？
8. 为什么一般不进行转换？

package org.example;

import java.util.Stack;

public class Test {

    // Recursive method to compute the sum of numbers from 1 to n
    int digui(int n, int res) {
        if (n == 1) {
            return res + 1;
        }
        res = n + res;
        return digui(n - 1, res);
    }

    // Improved recursive method to compute the sum of numbers from 1 to n
    int diguiAdvanced(int n, int res) {
        if (n == 1) {
            return res + 1;
        }
        return diguiAdvanced(n - 1, n + res);
    }

    // Recursive method to compute the nth Fibonacci number
    int diguiTree(int n) {
        if (n == 1 || n == 2) {
            return n - 1;
        }
        return diguiTree(n - 1) + diguiTree(n - 2);
    }

    // Iterative method to compute the sum of numbers from 1 to n using a stack
    int forLoopRecur(int n) {
        int res = 0;
        Stack<Integer> integers = new Stack<>();
        for (int i = 0; i <= n; i++) {
            integers.push(i);
        }
        while (!integers.isEmpty()) {
            int x = integers.pop();
            res += x;
        }
        return res;
    }

    public static void main(String[] args) {
        Test test = new Test();

        System.out.println("Result of digui: " + test.digui(5, 0));
        System.out.println("Result of diguiAdvanced: " + test.diguiAdvanced(5, 0));
        System.out.println("The 6th Fibonacci number: " + test.diguiTree(6));
        System.out.println("Sum of numbers up to 5 using iteration: " + test.forLoopRecur(5));
    }
}

时间复杂度 2.3

1. 在某平台如何评估简单行为的运行时间？加法 乘法 打印各需要多少nm？这个方法是否好呢？
2. 时间复杂度的计算是以具体的时间吗？不是的话 是什么
3. 你如何理解算法复杂度统计趋势的？举例说明
4. 这种算法复杂度的统计方法 有何优点
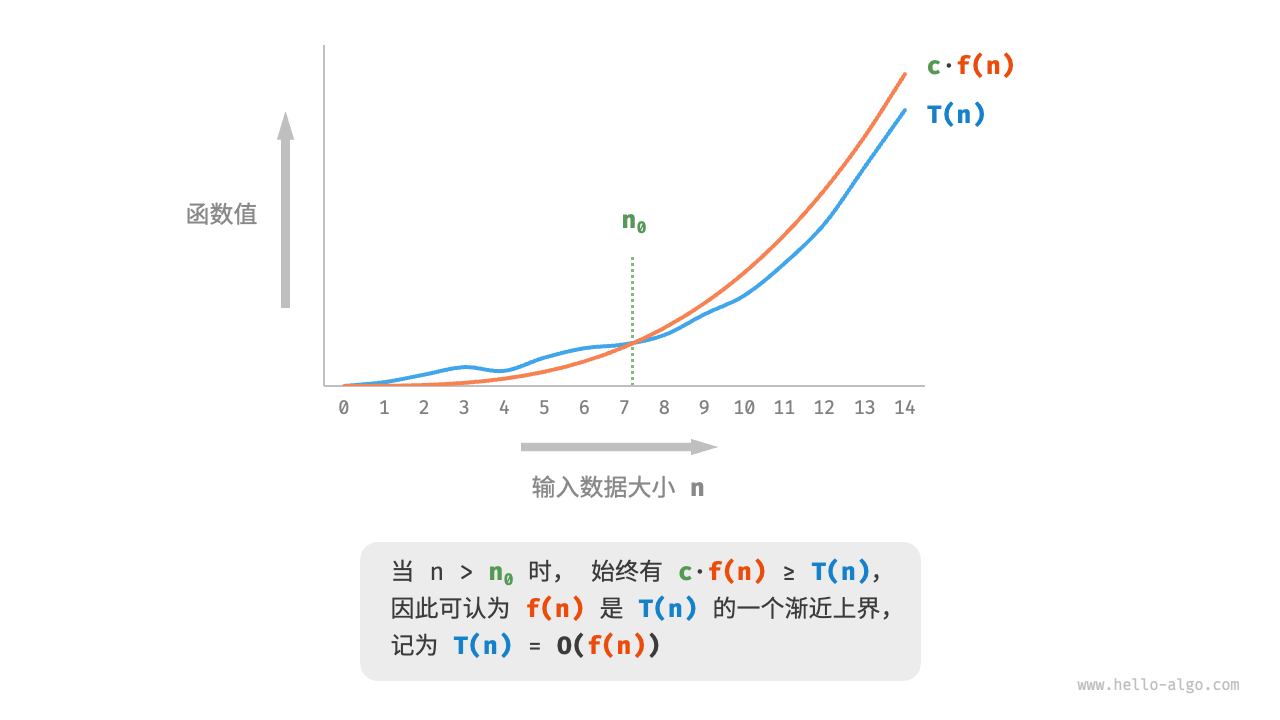
5. 时间复杂度本质上是计算什么，数学定义？（可以画出函数图像即可）
6. 算法复杂度， 以及常见无穷大的比较？
7. 写两种时间复杂度是2^n^ 的代码的例子
8. 列举一个时间复杂度是logn 的例子
9. 线性对数阶的例子
10. 阶乘例子
11. 时间复杂度分几种， 一般使用哪一种时间复杂度，为什么

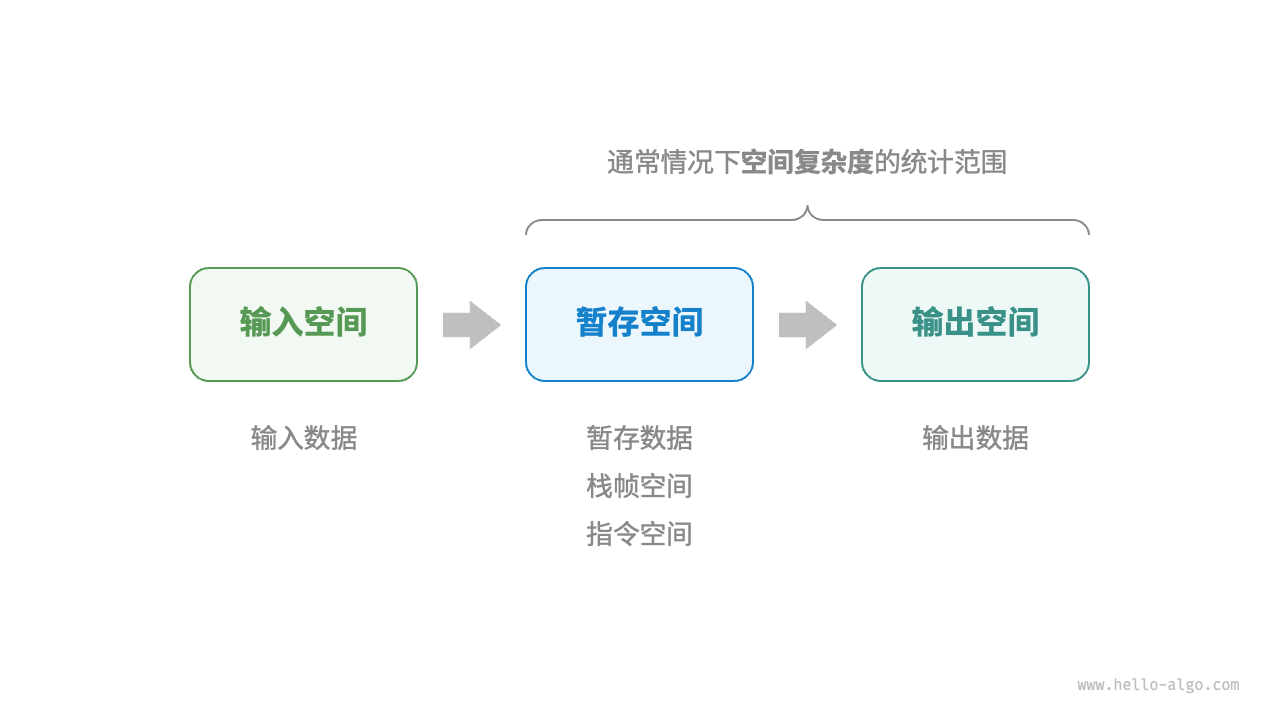
空间复杂度 2.4

1. 内存空间有几种？暂存空间又可以分为几种
2. 通常情况下我们统计哪些空间复杂度？
3. 请你画出结构图

4. 请你分别指出代码中对应的结构

   /* 类 */
   class Node {
       int val;
       Node next;
       Node(int x) { val = x; }
   }
   
   /* 函数 */
   int function() {
       // 执行某些操作...
       return 0;
   }
   
   int algorithm(int n) {        // ?
       final int a = 0;          // ?
       int b = 0;                // ?
       Node node = new Node(0);  // ?
       int c = function();       // ?
       return a + b + c;         // ?
   }

5. 空间复杂度中最差的含义是什么？

6. 判断下面代码的空间复杂度, 并解释为什么

int function() {
    // 执行某些操作
    return 0;
}
/* 循环的空间复杂度为 ? */
void loop(int n) {
    for (int i = 0; i < n; i++) {
        function();
    }
}
/* 递归的空间复杂度为 ? */
void recur(int n) {
    if (n == 1) return;
    return recur(n - 1);
}

6. 平方阶常见于什么数据结构？ 尝试创建一个二位链表
7. 如何使用递归占用二次空间
8. 对数阶举例

小结 2.5

算法效率评估

• 时间效率和空间效率是衡量算法优劣的两个主要评价指标。
• 我们可以通过实际测试来评估算法效率，但难以消除测试环境的影响，且会耗费大量计算资源。
• 复杂度分析可以消除实际测试的弊端，分析结果适用于所有运行平台，并且能够揭示算法在不同数据规模下的效率。

时间复杂度

• 时间复杂度用于衡量算法运行时间随数据量增长的趋势，可以有效评估算法效率，但在某些情况下可能失效，如在输入的数据量较小或时间复杂度相同时，无法精确对比算法效率的优劣。
• 最差时间复杂度使用大 𝑂 符号表示，对应函数渐近上界，反映当 𝑛 趋向正无穷时，操作数量 𝑇(𝑛) 的增长级别。
• 推算时间复杂度分为两步，首先统计操作数量，然后判断渐近上界。
• 常见时间复杂度从低到高排列有 𝑂(1)、𝑂(log⁡𝑛)、𝑂(𝑛)、𝑂(𝑛log⁡𝑛)、𝑂(𝑛2)、𝑂(2𝑛) 和 𝑂(𝑛!) 等。
• 某些算法的时间复杂度非固定，而是与输入数据的分布有关。时间复杂度分为最差、最佳、平均时间复杂度，最佳时间复杂度几乎不用，因为输入数据一般需要满足严格条件才能达到最佳情况。
• 平均时间复杂度反映算法在随机数据输入下的运行效率，最接近实际应用中的算法性能。计算平均时间复杂度需要统计输入数据分布以及综合后的数学期望。

空间复杂度

• 空间复杂度的作用类似于时间复杂度，用于衡量算法占用内存空间随数据量增长的趋势。
• 算法运行过程中的相关内存空间可分为输入空间、暂存空间、输出空间。通常情况下，输入空间不纳入空间复杂度计算。暂存空间可分为暂存数据、栈帧空间和指令空间，其中栈帧空间通常仅在递归函数中影响空间复杂度。
• 我们通常只关注最差空间复杂度，即统计算法在最差输入数据和最差运行时刻下的空间复杂度。
• 常见空间复杂度从低到高排列有 𝑂(1)、𝑂(log⁡𝑛)、𝑂(𝑛)、𝑂(𝑛2) 和 𝑂(2𝑛) 等。

Q：尾递归的空间复杂度是 𝑂(1) 吗？

理论上，尾递归函数的空间复杂度可以优化至 𝑂(1) 。不过绝大多数编程语言（例如 Java、Python、C++、Go、C# 等）不支持自动优化尾递归，因此通常认为空间复杂度是 𝑂(𝑛) 。

Q：函数和方法这两个术语的区别是什么？

函数（function）可以被独立执行，所有参数都以显式传递。方法（method）与一个对象关联，被隐式传递给调用它的对象，能够对类的实例中包含的数据进行操作。

下面以几种常见的编程语言为例来说明。

• C 语言是过程式编程语言，没有面向对象的概念，所以只有函数。但我们可以通过创建结构体（struct）来模拟面向对象编程，与结构体相关联的函数就相当于其他编程语言中的方法。
• Java 和 C# 是面向对象的编程语言，代码块（方法）通常作为某个类的一部分。静态方法的行为类似于函数，因为它被绑定在类上，不能访问特定的实例变量。
• C++ 和 Python 既支持过程式编程（函数），也支持面向对象编程（方法）。

Q：图解“常见的空间复杂度类型”反映的是否是占用空间的绝对大小？

不是，该图展示的是空间复杂度，其反映的是增长趋势，而不是占用空间的绝对大小。

假设取 𝑛=8 ，你可能会发现每条曲线的值与函数对应不上。这是因为每条曲线都包含一个常数项，用于将取值范围压缩到一个视觉舒适的范围内。

在实际中，因为我们通常不知道每个方法的“常数项”复杂度是多少，所以一般无法仅凭复杂度来选择 𝑛=8 之下的最优解法。但对于 𝑛=85 就很好选了，这时增长趋势已经占主导了。

3 数据结构

• 数据结构的分类
• 基本数据类型
• 数字编码
• 字符编码
• 小结

数据结构分类3.1

1. 常见的数据结构有哪8个，从哪两个维度进行分类？
2. 从逻辑结构怎么分？更进一步怎么分
3. 从物理结构怎么分？又以什么为代表
4. 所有数据结构的 底层是什么

基本数据类型 3.2

1. 基本数据类型有什么特点？具体谈一谈
2. 基本数据类型的占用空间和取值范围？
3. 布尔类型为什么占用1 byte
4. 基本数据类型和数据结构有什么关系？
5. 负数为什么使用补🐎存储？
6. java 中对于int 类型的数据是否有缓存的策略

使用补码参与运算后，无需再管符号位，可以让符号位直接参与运算。这就是使用补码的最大的好处。

数字编码 3.3

1. 为什么所有整数类型能够表示的负数都比正数多一个
2. 为什么int 和 flout长度相同，但是flout的长度> int， 这样做的代价是什么

字符编码 3.4

1. 简单介绍ASCll码【地位，几位， 缺陷】？
2. 在GBK的方案中， ASCll 和汉字分别使用几个字节表示？
3. Unicode 是为了解决什么问题？
4. Unicode 是否规定了如何存储字符的码点，如何解决
5. 简单介绍 UTF-8 的核心特性
6. UTF-8 的编码规则（分情况讨论， 说明具体的方式）
7. 程序运行中的字符串采用什么编码方式？
8. 这种方式有什么特点？
9. 字符串在编程语言中的 存储方式和其在文件存储或者网络传输中是否是相同的问题？不是的话，后者一般如何编码

小结 3.5

1. 重点回顾¶

• 数据结构可以从逻辑结构和物理结构两个角度进行分类。逻辑结构描述了数据元素之间的逻辑关系，而物理结构描述了数据在计算机内存中的存储方式。
• 常见的逻辑结构包括线性、树状和网状等。通常我们根据逻辑结构将数据结构分为线性（数组、链表、栈、队列）和非线性（树、图、堆）两种。哈希表的实现可能同时包含线性数据结构和非线性数据结构。
• 当程序运行时，数据被存储在计算机内存中。每个内存空间都拥有对应的内存地址，程序通过这些内存地址访问数据。
• 物理结构主要分为连续空间存储（数组）和分散空间存储（链表）。所有数据结构都是由数组、链表或两者的组合实现的。
• 计算机中的基本数据类型包括整数 byte、short、int、long ，浮点数 float、double ，字符 char 和布尔 bool 。它们的取值范围取决于占用空间大小和表示方式。
• 原码、反码和补码是在计算机中编码数字的三种方法，它们之间可以相互转换。整数的原码的最高位是符号位，其余位是数字的值。
• 整数在计算机中是以补码的形式存储的。在补码表示下，计算机可以对正数和负数的加法一视同仁，不需要为减法操作单独设计特殊的硬件电路，并且不存在正负零歧义的问题。
• 浮点数的编码由 1 位符号位、8 位指数位和 23 位分数位构成。由于存在指数位，因此浮点数的取值范围远大于整数，代价是牺牲了精度。
• ASCII 码是最早出现的英文字符集，长度为 1 字节，共收录 127 个字符。GBK 字符集是常用的中文字符集，共收录两万多个汉字。Unicode 致力于提供一个完整的字符集标准，收录世界上各种语言的字符，从而解决由于字符编码方法不一致而导致的乱码问题。
• UTF-8 是最受欢迎的 Unicode 编码方法，通用性非常好。它是一种变长的编码方法，具有很好的扩展性，有效提升了存储空间的使用效率。UTF-16 和 UTF-32 是等长的编码方法。在编码中文时，UTF-16 占用的空间比 UTF-8 更小。Java 和 C# 等编程语言默认使用 UTF-16 编码。

2. Q & A¶

Q：为什么哈希表同时包含线性数据结构和非线性数据结构？

哈希表底层是数组，而为了解决哈希冲突，我们可能会使用“链式地址”（后续“哈希冲突”章节会讲）：数组中每个桶指向一个链表，当链表长度超过一定阈值时，又可能被转化为树（通常为红黑树）。

从存储的角度来看，哈希表的底层是数组，其中每一个桶槽位可能包含一个值，也可能包含一个链表或一棵树。因此，哈希表可能同时包含线性数据结构（数组、链表）和非线性数据结构（树）。

Q：char 类型的长度是 1 字节吗？

char 类型的长度由编程语言采用的编码方法决定。例如，Java、JavaScript、TypeScript、C# 都采用 UTF-16 编码（保存 Unicode 码点），因此 char 类型的长度为 2 字节。

Q：基于数组实现的数据结构也称“静态数据结构” 是否有歧义？栈也可以进行出栈和入栈等操作，这些操作都是“动态”的。

栈确实可以实现动态的数据操作，但数据结构仍然是“静态”（长度不可变）的。尽管基于数组的数据结构可以动态地添加或删除元素，但它们的容量是固定的。如果数据量超出了预分配的大小，就需要创建一个新的更大的数组，并将旧数组的内容复制到新数组中。

Q：在构建栈（队列）的时候，未指定它的大小，为什么它们是“静态数据结构”呢？

在高级编程语言中，我们无须人工指定栈（队列）的初始容量，这个工作由类内部自动完成。例如，Java 的 ArrayList 的初始容量通常为 10。另外，扩容操作也是自动实现的。详见后续的“列表”章节。

Q：原码转补码的方法是“先取反后加 1”，那么补码转原码应该是逆运算“先减 1 后取反”，而补码转原码也一样可以通过“先取反后加 1”得到，这是为什么呢？

这是因为原码和补码的相互转换实际上是计算“补数”的过程。我们先给出补数的定义：假设 𝑎+𝑏=𝑐 ，那么我们称 𝑎 是 𝑏 到 𝑐 的补数，反之也称 𝑏 是 𝑎 到 𝑐 的补数。

给定一个 𝑛=4 位长度的二进制数 0010 ，如果将这个数字看作原码（不考虑符号位），那么它的补码需通过“先取反后加 1”得到：

0010→1101→1110

我们会发现，原码和补码的和是 0010+1110=10000 ，也就是说，补码 1110 是原码 0010 到 10000 的“补数”。这意味着上述“先取反后加 1”实际上是计算到 10000 的补数的过程。

那么，补码 1110 到 10000 的“补数”是多少呢？我们依然可以用“先取反后加 1”得到它：

1110→0001→0010

换句话说，原码和补码互为对方到 10000 的“补数”，因此“原码转补码”和“补码转原码”可以用相同的操作（先取反后加 1 ）实现。

当然，我们也可以用逆运算来求补码 1110 的原码，即“先减 1 后取反”：

1110→1101→0010

总结来看，“先取反后加 1”和“先减 1 后取反”这两种运算都是在计算到 10000 的补数，它们是等价的。

本质上看，“取反”操作实际上是求到 1111 的补数（因为恒有 原码 + 反码 = 1111）；而在反码基础上再加 1 得到的补码，就是到 10000 的补数。

上述以 𝑛=4 为例，其可被推广至任意位数的二进制数。

4 数组与链表

数组 4.1

1. 什么是数组？线性数据结构，用来存储相同类型数据在连续空间
2. 数组的特点，（两个，线性 和连续与否）
3. 初始化数组的两种操作 java

int shuzu = new int[5];

4. 索引的本质是什么？
5. 如何随机访问元素？
6. 如何插入元素
7. 如何删除元素
8. 删除元素完成后，我们是否需要特意去修改原先末尾的元素？
9. 数组的插入和删除操作有什么缺点
10. 遍历数组的两种方式分别是什么？
11. 如何在数组中找到特定的元素
12. 如何进行数组扩容？
13. 数组的优点和局限性
14. 数组的应用有哪些？

链表 4.2

1. 对比数组最显著的优势是什么情况下体现的
2. 链表是什么
3. 节点之间通过什么链接
4. 如何使用java 创建一个链表类
5. 如何初始化一个链表
6. 一个链表通常如何表示？（使用什么当作代称？）
7. 链表如何删除节点， 删除n0后面的第一个节点？ 这样是否会多余一个节点的内存
8. 如何访问节点？

赏

a cup of coofee

微信